Article by: Sean
Article applies to: all models with the M70 V12 engine.
Problem: People who often visiting this site are probably aware of my ongoing problems with hesitating, surging, running rough, erratic idle, hunting idle and stalling when accelerating. Folks who have some years of experience with working on cars are saying now: false (un-metered) air bypassing the MAF and letting the engine run lean. For example, a cracked crankcase ventilation hose. I know..I know.. but I checked out the obvious things already….over and over again. And again, to be sure.
What gave me the most headache was that both banks where suffering from this problem. I disconnected 6 injectors of each bank, but the engine was running rough on left and right. So it had to be something both banks are sharing. But besides the EML computer, exhaust, timing chain, crankshaft and fuel return hose there aren’t many components that both banks share and can produce such a problem.
It kept spinning in my mind that it had to do something with the mixture, the erratic idle (‘hunting’) was the problem behind this thought. The engine was getting to much air or not enough fuel. I checked the air supply already, maybe the amount of injected fuel wasn’t correct. So I clamped off the fuel return hose (see section ‘fuel pressure regulators’) in order to raise the fuel system pressure by hand. Suddenly the engine started to run normal. At that moment, I realized that the fuel system pressure was probably to low (I unfortunately don’t have any equipment to measure fuel pressure).
So I replaced the fuel pressure regulators (see section ‘fuel pressure regulators’). That didn’t solve the problem. The pressure in the fuel system is supplied by the fuel pumps. Maybe they delivered not enough pressure. One pump died already by age, so I replaced both (see section ‘fuel pump replacement’) just to be sure. That didn’t solve the problem. The only thing that was left where the fuel filters, perhaps they where clogged. They where old old, so I replaced them (see section ‘fuel filter replacement’). That didn’t solve the problem. I don’t recommend this kind of monkey testing, but I didn’t had the proper test equipment and was running desperate now.
I had spent almost half of my monthly salary on parts and I was back to the beginning, with no clue where to start troubleshooting now. I noticed I started to look at some ads for a 12 year old nice Benz S or Lexus 400, getting my wife real nervous that yet another car will be purchased (we have 4 cars now and seriously running out of space here).
But I don’t give up very quickly and was still convinced it had something to do with the amount of injected fuel. So if fuel the system pressure was right (I mean, virtually every component is replaced now so it had to be good), maybe several injectors where clogged. So I removed the fuel rails (with injectors), applied fuel pressure and tested every injector shortly with 12 volt. Every injector worked like a charm, spraying a nice pattern of fuel in the air….d#$@#mn car!!!
The only thing that was left and I could think of where the MAF’S. They are determining how much air is sucked into the engine and give the DME’s a signal so they can calculate the amount of injected fuel (by controlling the time the fuel injectors are open)….but both MAF’s??? I swapped them already from one bank another without any improvement. Also, they where glowing and according to Bentleys: ‘if the wire glows, the air flow sensor and ECM are probably operating correctly‘. Hugh mistake. Big mistake.
One particular day, I purchased a second hand radiator (see section ‘radiator replacement’) from a guy who scrapped a 750. He also had some other parts, which I bought too. Including some MAF’s…he offered me a reasonable price and it’s always nice to have some spare parts. Back at home, I replaced the MAF’S without much confidence, just to eliminate another cause of all my problems. I started the engine….and it ran as new. Both my MAF’s where shot. It took me months to find this one. And after some investigation, it turned out that I simply could have measured my defective MAF’s with a simple voltmeter. I just overlooked that one. This section is about measuring the MAF’s so other people won’t make this stupid mistake.
Background:
This picture shows a cut-trough view of the air-mass sensor:
The air-mass sensor is completely electronic, no moving parts. It’s also known as the hot-wire sensor. The sensor exists basically out of 2 parts: (1) is air intake temperature sensor and (2) is the heated wire.
The hot wire is heated to 100 degrees Celsius (180 F) above incoming air temperature when the ignition is turned on. So on a hot day, if the ambient air is about 30 degrees Celsius (86 F) the hot wire is heated up to 130 degrees Celsius (266 F). It doesn’t glow at that moment. When you open the throttle, intake air flows over the hot wire and cooling the wire down. With more air passing the heated wire, the cooling effect is greater. The control circuit of the MAF is trying to keep the hot wire at the same original temperature of 100 degrees Celsius above ambient temperature. So the control circuit is applying more current flowing through the heated wire. This current is measured and converted into a voltage signal, which gives the DME an indication how much air is sucked into the engine.
Hit the gas -> open throttle body -> allowing more air sucked into the engine -> the air is cooling the heated wire -> MAF is keeping the heated wire at the same temperature by increasing current flow through heated wire -> current flow is converted into a flat DC signal. This process is performed within 1 millisecond.
When the air-mass sensor is working normal, the hot wire does not glow. To burn off any deposits and dirt, the control system will heat the wire red hot to 1000 degrees Celsius (1800 F) for about 1 second, after you shut off your engine. This is the cleaning process and only performed if the engine is revved up to at least 2000 rpm. So starting your engine, let it idle for a certain time and shut off means no hot wire cleaning.
One remark must be made: I hear very often that these heated wire MAF’s are killed by using K&N filters. Jon Holdsworth about this issue:
“A well lubed K&N filter will deposit K&N oil on the MAF sensor wire and cause more of the wire to burn off at each shutdown, eventually destroying the sensor. Common consensus is to ditch the K&N and use the good ole paper filter.”
Richard Arligde:
“You’ve probably heard like me that using after market oiled-foam air cleaners are not conducive to long MAF life.”
And one last remark by me: do not try to clean the hot wire. It will break. Don’t ask me how I know that.
How to troubleshoot:
The very first thing to check is of your MAF’s are glowing. Remove MAF at one side, leave wiring harness connected and place the MAF somewhere upon the engine (intake manifold) so you can look at it.
Prevent that the MAF falls off the engine (I used the air filter box for this). Start your engine, it will run in limp mode because only the other cylinder bank is working, rev it up to 2000 rpm, let it idle and shut it off. You should see something like this:
The picture was shot through the windscreen, sorry for the poor quality. If you look careful, you’ll see the wire glow for just a second. Reinstall this MAF and test the other side.
The MAF has a 6 terminal electrical connector, it has some very fine pine numbers located on the plug, not visible because the camera was out of focus:
Measurements are performed at this connector. Reattach the connectors, pull the rubber boot back on the backside of the connectors.
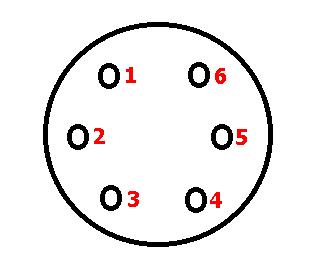
The terminals are numbered like this (looking at the backside of the connector towards the MAF):
First, you must know that these particular MAF’s are producing a flat DC signal and they can be tested with a normal digital multi-meter.
These MAF’s don’t produce frequency signals so you don’t need to use an oscilloscope.
The next picture shows how to test:
Close-up, if you look closely you’ll see the numbers indicating the terminals:
You test with a heated up engine running at idle and revving up to 2000 rpm. Do not rev the engine above this due to premature A-clutch failures of your transmission.
Correct procedure (if you just drove it) is: put tranny in P, shut the engine down for at least 10 minutes to release the hydraulic pressure inside your tranny, start the car (don’t drive it!) in P and keep it in P.
Maybe I am a bit @n@l-retentive about this, but the transmission was toasted before (totally burned A-clutch pack) so I don’t take any risk. You should measure the following (readings may vary just a very little bit, depending from engine to engine):
| Terminal | Value |
| 1 | ~0.78 volt, virtually not fluctuating while revving engine |
| 2 | +12 volt battery voltage |
| 3 | +5 volt steady voltage |
| 4 | Ground |
| 5 | ~0.27 volt, slightly rises to 0.33 volt when revving to 2000 rpm |
| 6 | this is the actual mixture signal: ~2.35 volt when idling to ~2.7 volt at 2000 rpm |
In my case, the 5 volt voltage at terminal 3 was 1.405 volt (as the photo above shows) instead of the 5 volt. This indicated for me a bad MAF.
Remark from Sean: later on, I received emails from people who are telling me that they also measure 1,4 volt at terminal #3 and they don’t experience any problems at all:
Jeff Greenfield about this: “I will tell you, that after replacing both MAF’s I still had approx. 1.4 volts at terminal 3 with the engine running. I did verify that there is 5 volts here with the MAF disconnected. What I did discover is that the voltage at terminal 3 will change some if you diddle the mixture screw, however in my case I could not get it as high as 5 volts.”Note from Sean: I suggest you don’t fiddle with the mixture screw. These MAF’s are factory calibrated and normally you don’t have to adjust them.
Richard Arlidge about this: “Yes, I get the correct readings at the connector face and the hot wire glows fine, but stick the connector together and read the back-end of pin 3 and hey, presto, 1.4V instead of 5V like yours. I am not in a hurry to race out and buy a couple of new ones”
The mystery about terminal #3 is still under investigation. It is sure that I am measuring a solid 5 volt (checked several times) with a running engine and a connected MAF. BUT: my car could hardly be driven due to hesitation, surging and stalling. If you experience such problems, maybe it’s a screwed MAF. If you just experience a rough idle (or something like that) but the car is running fine while driving, it isn’t likely that your MAF is shot, even when you measure 1,4 volt at #3.
Richard Arlidge getting back: “Thought I’d drop you a line to update you. Yes, I can’t understand the difference in the measured voltage – mine are definitely only 1.4V at the back of the plug when connected, but 5V at the pin when disconnected. Returning to the MAF’s, at the end of the day it’s the pin 6 out voltage (mixture control) which is all important. I would suggest you add something to your page to this effect. I ran a lead back to my digital multimeter into the car (from the back of the connector) and took it for a run. On both sides I measured the output voltage which progressively increased as the load/rpms went up. While my car wasn’t pulling more than about 5000 rpms at the time, both were going north of about 4.2V and I gather they should get close to 5V at max rpm. If they’re progressively increasing and reading over 4V, I suspect anyone who is experiencing running problems look for another cause, because it is unlikely to be the MAFs. If they not reading a steadily increasing pin 6 output, apart from cleaning all the connections, checking the wire’s not broken; that they’re glowing after turn off and the readings on the various pins are as you state, then they’re either stuffed, or contaminated with oil etc. I would suggest spraying them with a proprietary carb cleaner or residue-free drying electrical cleaner. As you have said, do not try to mechanically clean them.
Note from Sean: using aggressive carb cleaner looks like a risk to me. These hot wires are extremely sensitive and I can’t predict the consequences!
The supply voltages at terminal 2 and 3 can also be measured with a removed connector:
Now it’s showing the correct value. As soon as I reconnected the plug, voltage dropped to 1.405 volt. To accomplish the testing,
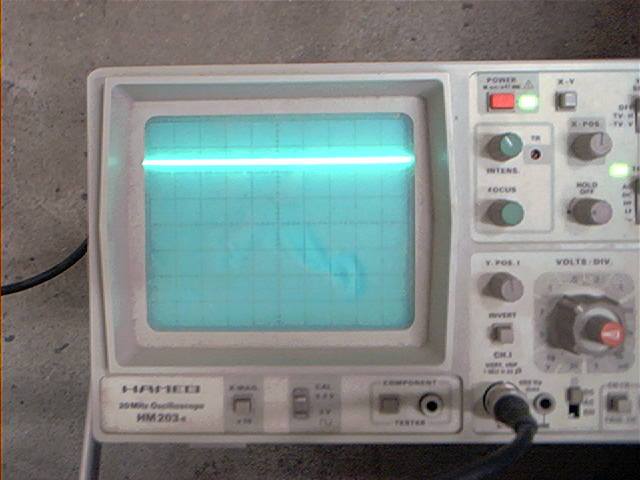
I also hooked up an oscilloscope to the MAF, ensuring that it isn’t producing frequency signals:
And it wasn’t (tested every terminal):
I like extensive testing. The next picture shows the testing with several MAF’s:
I certainly hope this story will assist you while testing your MAF’s and prevent fighting an expensive battle like I did, when I tried to solve my problems.
Moral of this story: measure before replacing parts instead of the other way around.


![Bosch_MAF[1]](https://www.shiftbmw.com/wp-content/uploads/2013/12/Bosch_MAF1.gif)